Boston Construction Permits

Construction permit data in Boston - where are investments going?

I have started looking for a property in Boston. With many of its self-claimed “up and coming” neighborhoods, it can be tricky to locate the next most profitable investment. Of course one way to make money is to chase money; where there are already lots of investment would probably see the highest appreciation. Therefore, I leveraged the Boston construction permits data published by the /data.boston.gov to hopeful identify where the investments are going

import pandas as pd
import geopandas as gpd
from geopandas import GeoDataFrame
import numpy as np
import matplotlib.pyplot as plt
from shapely.geometry import Point
from shapely.geometry import Polygon
import os
import datetime as dt
import contextily as ctx
import rasterio as rio

os.chdir(r'C:\Users\zkuang\PycharmProjects\FIndAHouse')
house_only = True # only look at new houses
new_construnction_only = False # only look at new construction

Geopandas is a spatial analysis tool in python. I had problems installing it with pip but anaconda did the magic. Contextily is used for adding the basemap.

Permit data

permit_raw = pd.read_csv(r'tmpvnqj4wz3.csv')
permit = permit_raw.drop(['permittypedescr','comments','applicant','status','owner','state','property_id','parcel_id'],axis = 1)
permit['issued_year'] = [int(i.split('-')[0]) for i in permit.issued_date] # add a permit issued year num

permit.head()

	permitnumber	worktype	description	declared_valuation	total_fees	issued_date	expiration_date	occupancytype	sq_feet	address	city	zip	lat	long	issued_year
0	A100071	COB	City of Boston	40000.00	429.0	2011-11-04 11:04:58	2012-05-04 00:00:00	Comm	170.0	175 W Boundary RD	West Roxbury	02132	42.26075	-71.14961	2011
1	A1001201	INTEXT	Interior/Exterior Work	74295.75	803.0	2019-11-13 13:38:56	2020-05-13 00:00:00	Multi	0.0	211 W Springfield ST	Roxbury	02118	42.34060	-71.08025	2019
2	A100137	EXTREN	Renovations - Exterior	15000.00	206.0	2013-01-03 14:13:09	2013-07-03 00:00:00	1-2FAM	0.0	14 William Jackson AVE	Brighton	02135	42.34460	-71.15405	2013
3	A1001913	INTREN	Renovations - Interior NSC	1.00	33.0	2019-10-18 09:21:00	2020-04-18 00:00:00	Comm	0.0	130-140 Brighton AVE	Allston	02134	42.35276	-71.13185	2019
4	A1002445	INTREN	Renovations - Interior NSC	50000.00	556.0	2019-11-12 11:00:03	2020-05-12 00:00:00	1-2FAM	0.0	7 Amboy ST	Allston	02134	42.35971	-71.12433	2019

permit.shape

(449358, 15)

Each permit comes with some key information such as it’s location (long, lat), description, occupancy type and declared value that are relevant to our quest. There are quite a lot of permits outstanding (449358, well done BOS).

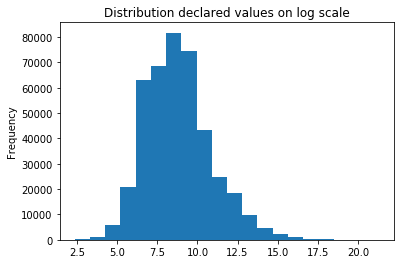
We noticed a lot of projects that has 0 declared value that are not relevant in our quest. We plot a declared value distribution without those entries. We noticed a long tail even on the log scale — some of the property values are just way up there!

np.log(permit[permit.declared_valuation > 10].declared_valuation).plot(
    kind='hist',title = 'Distribution declared values on log scale', bins = 20)

<matplotlib.axes._subplots.AxesSubplot at 0x24d4d913d08>

permit.occupancytype.value_counts().head(5)

1-2FAM    140025
Comm      138222
Multi      47668
1-3FAM     46674
Mixed      17944
Name: occupancytype, dtype: int64

The most common occupancy type 1-2 family houses, followed by commercial constructions and multi family properties.

permit.description.value_counts().head(5)

Electrical                    93709
Plumbing                      59700
Gas                           44368
Renovations - Interior NSC    39010
Low Voltage                   33194
Name: description, dtype: int64

permit.groupby('description').mean()['declared_valuation'].sort_values(ascending = False).head(10)

description
New construction          8.401808e+06
Erect                     7.591059e+06
Addition                  1.613690e+06
Fast Track Application    1.082881e+06
City of Boston            8.492774e+05
Change Occupancy          6.806303e+05
Commercial Parking        5.283526e+05
Industrial Boiler         2.647291e+05
Interior/Exterior Work    2.328353e+05
Industrial Furnace        2.141444e+05
Name: declared_valuation, dtype: float64

The most common project type is electrical work. Not exactly construction here. Although expectedly, the most valualbe projects are new constructions, erect, additions

permit.issued_year.plot(kind='hist')

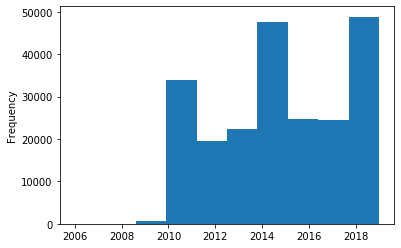
Finally, we found most of the permits are issued after 2010, which means the corresponding project is likely to still be relevant to today’s market (2019).

Create maps using grids

With the baseline understanding of our data, we are ready to create the value plot. First, we define our help functions to create the grids we needed for spatial merge.

def create_grids(geo_df,n = 100):
    '''Creating a grid of n by n that covers the input geo feature geo_df'''
    crs = geo_df.crs
    x_range = [min(geo_df.long),max(geo_df.long)]
    y_range = [min(geo_df.lat),max(geo_df.lat)]

    x_grids = np.arange(x_range[0],x_range[1],step = (x_range[1] - x_range[0])/n)
    y_grids = np.arange(y_range[0],y_range[1],step = (y_range[1] - y_range[0])/n)

    grids = []

    for i in range(len(x_grids)-2):
        for j in range(len(y_grids)-2):
            grids.append(Polygon(zip([x_grids[i],x_grids[i],x_grids[i+1],x_grids[i+1]],
                                     [y_grids[j],y_grids[j+1],y_grids[j+1],y_grids[j]])))

    geo_grids = GeoDataFrame([],crs = crs,geometry = grids)
    return geo_grids

def geo_join(geo_df, n):
    geo_grids = create_grids(geo_df,n = n)
    geo_join = gpd.sjoin(geo_df,geo_grids,how = 'inner',op='within')
    return geo_join

The follow cell gives us the option to further filter down the desired permit types in our study

Now we are ready to create our spatial objects. This turns our permit data into a geodataframe. Right now it’s just dots with no fine-tuned feature to display. We use EPSG:2805 (Massachusetts mainland) projected coordinate system. crs is not a necessary argument in creating GeoDataFrame, but I found it helpful in aligning our geodataframe to our basemaps.

permit_clean = permit[(~pd.isna(permit.long)) & (~pd.isna(permit.lat))
                      & (~pd.isna(permit.declared_valuation))]

geometry = [Point(xy) for xy in zip(permit_clean.long, permit_clean.lat)]
crs = {'init':'epsg:2805'}
geo_permit = GeoDataFrame(permit_clean,geometry = geometry,crs = crs)
geo_permit.plot()

geometry = [Point(xy) for xy in zip(permit_clean.long, permit_clean.lat)]
crs = {'init':'epsg:2805'} # crs be consistent
geo_permit = GeoDataFrame(permit_clean,geometry = geometry,crs = crs)
geo_grids = create_grids(geo_permit,100)

GeoPandas created simple spatial join function. When joining point features to shapefiles, specifying op = "within" can significantly reduce computational burden.

geo_join = gpd.sjoin(geo_permit, geo_grids, how='inner', op='within')

We use pandas groupby function to get a mean declared value within each grid cell. Then, We are specifying some fine tuning to get our dataset ready for plotting, such as filtering out NA mean declared values and extreme values such as ones out of [0.05, 0.95] quantile. And finally, we transfer the mean declared value to a log scale.

reported_value = geo_join.groupby('index_right').mean()['declared_valuation']
geo_grids_value = geo_grids.merge(reported_value,how = 'left',left_index = True,right_index=True)
# here we are joining by index, which are indices inherited from the geo_grids object
geo_grids_value = geo_grids_value[~pd.isna(geo_grids_value.declared_valuation)]
geo_grids_value = geo_grids_value[(geo_grids_value.declared_valuation > np.percentile(geo_grids_value.declared_valuation, 5))
                                  & (geo_grids_value.declared_valuation < np.percentile(geo_grids_value.declared_valuation, 97))]
geo_grids_value['declared_valuation_lg'] = np.log(geo_grids_value.declared_valuation+0.01)

Here we are adding a few extra features to plot

high value commercial construction (declared valuation > \(10^6\) USD)
high value public investment (investment made by City of Boston with value > \(10^6\) USD)

geometry_full = [Point(xy) for xy in zip(permit_raw.long, permit_raw.lat)]
crs = {'init':'epsg:2805'}
geo_permit_full = GeoDataFrame(permit_raw,geometry = geometry_full,crs = crs)


geo_permit_comm = geo_permit_full[(geo_permit_full.occupancytype == 'Comm')
                             & (geo_permit_full.declared_valuation > 1e6)
                             & (geo_permit_full.description.str.match("New.+"))]

public_invest = geo_permit_full[(geo_permit_full.description == 'City of Boston')
                           & (geo_permit_full.declared_valuation > 1e6)]

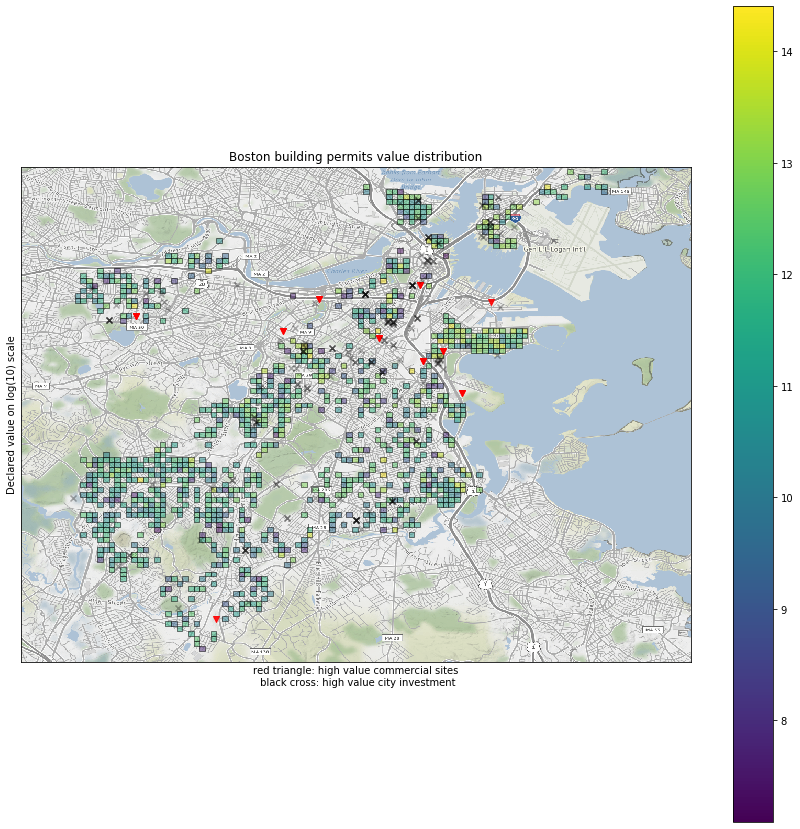
Finally we are ready to create the plot

def creat_base_map(geo_df,ax):
    w, s, e, n = geo_df.total_bounds
#    zoom = ctx.tile._calculate_zoom(w, s, e, n)
    image, extent = ctx.bounds2img(w, s, e, n, ll = True)
    ax.imshow(image, extent= (extent[0],extent[2],extent[1],extent[3]), alpha = 0.8,cmap=plt.get_cmap('gray'))
    return ax

_,ax = plt.subplots(1, figsize=(15,15))

ax = creat_base_map(geo_grids,ax)
geo_grids_value.plot(edgecolor='k', column='declared_valuation_lg', ax=ax, alpha=0.5, legend=True, label = 'Declared value on a log scale')
geo_permit_comm.plot(ax=ax, alpha=0.9, legend=True, color = 'r',label = 'high value commercial sites',marker = 'v')
public_invest.plot(ax=ax, alpha=0.3, legend=True, color = 'k',label = 'high value public investment',marker = 'x')

ax.set_title('Boston building permits value distribution')
ax.set_ylabel('Declared value on log(10) scale')
ax.set_xlabel('red triangle: high value commercial sites\n black cross: high value city investment')
plt.setp(ax.get_xticklabels(), visible=False)
plt.setp(ax.get_yticklabels(), visible=False)
ax.tick_params(axis='both', which='both', length=0)
plt.show()

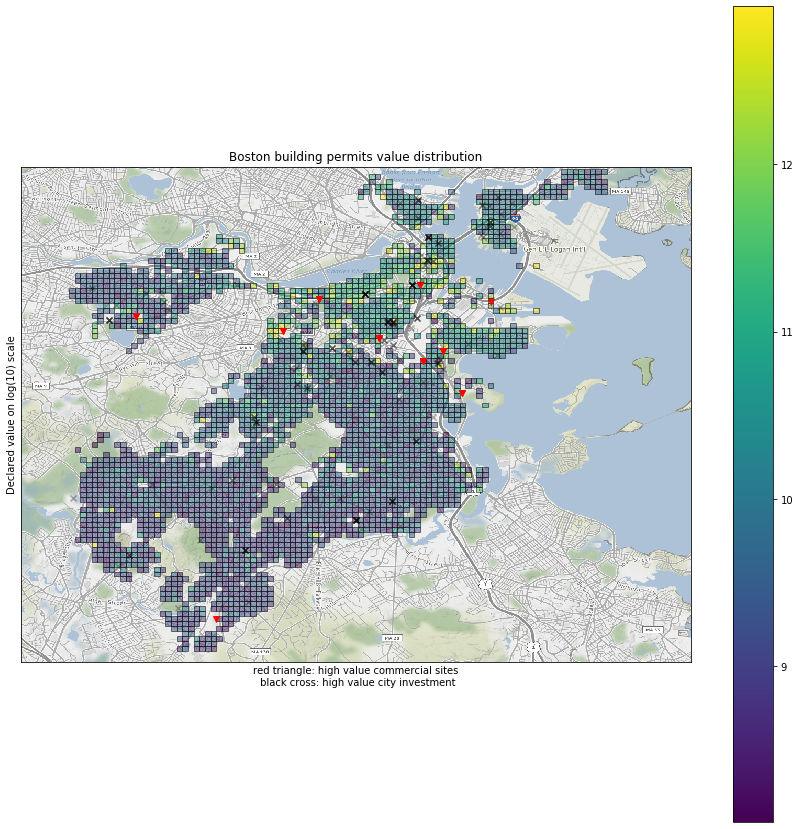
Observations

When all projects are considered, it is obvious that the downtown / Back Bay / Fenway area have the highest development value
Seaport \ Southie have a lot of high value properties under permit as well, standing in the second tier of development value
There are spread-out valuable development pockets in Dorchester and Jamaica Plain. Overall, it seems like Dorchester has a slight advantage of development value, especially for the areas along the MBTA Red line and freeway.

What if we filter for only new residential constructions?

Since I’m mostly interested in new constructions, it might be worthwhile to focus on only residential new constructions for a secondary analysis.

geo_join_filt = geo_join[(geo_join.occupancytype.str.match('(.+FAM|.unit|Mixed)')) &#matching multiple family units and mixed properties
                        (~pd.isna(geo_join.description)) &
                        (geo_join.description.str.match('(Addition|Erect|New construction)'))]# matching new constructions

reported_value_filt = geo_join_filt.groupby('index_right').mean()['declared_valuation']
geo_grids_value_filt = geo_grids.merge(reported_value_filt,how = 'left',left_index = True,right_index=True)
# here we are joining by index, which are indices inherited from the geo_grids object
geo_grids_value_filt = geo_grids_value_filt[~pd.isna(geo_grids_value_filt.declared_valuation)]
geo_grids_value_filt = geo_grids_value_filt[(geo_grids_value_filt.declared_valuation > np.percentile(geo_grids_value_filt.declared_valuation, 5))
                                  & (geo_grids_value_filt.declared_valuation < np.percentile(geo_grids_value_filt.declared_valuation, 95))]
geo_grids_value_filt['declared_valuation_lg'] = np.log(geo_grids_value_filt.declared_valuation+0.01)

_,ax = plt.subplots(1, figsize=(15,15))

ax = creat_base_map(geo_grids,ax)
geo_grids_value_filt.plot(edgecolor='k', column='declared_valuation_lg', ax=ax, alpha=0.5, legend=True, label = 'Declared value on a log scale')
geo_permit_comm.plot(ax=ax, alpha=0.9, legend=True, color = 'r',label = 'high value commercial sites',marker = 'v')
public_invest.plot(ax=ax, alpha=0.3, legend=True, color = 'k',label = 'high value public investment',marker = 'x')

ax.set_title('Boston building permits value distribution')
ax.set_ylabel('Declared value on log(10) scale')
ax.set_xlabel('red triangle: high value commercial sites\n black cross: high value city investment')
plt.setp(ax.get_xticklabels(), visible=False)
plt.setp(ax.get_yticklabels(), visible=False)
ax.tick_params(axis='both', which='both', length=0)
plt.show()

Observations

A lot of new constructions are happening in Southie and South JP
The Southie development value seems to spill out to North Dorchester along the T / freeway line

Beyond grids: KDEPLOT for density plots

The grid system is not smooth enough. I continued to experiment with KDEplot to estimate “density” of permit dots. Notice that default KDEplots coming with seaborn doesn’t take in weights, therefore we have to manually create oversampled dataset with regard to declared evaluation.

New construction density

import geoplot as gplt
permit_KDE = permit_clean[(permit_clean.declared_valuation > 100) & 
                          (permit_clean.description.str.match('(Addition|Erect|New construction)'))]
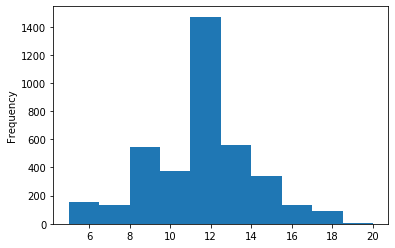
permit_KDE['w_col'] = np.floor(np.log(permit_clean.declared_valuation))
permit_KDE.w_col.plot(kind = 'hist')

Taking a look at the distribution of the integer log declared values in those new constructions.

df_point = permit_KDE[['long','lat','w_col']]
df_point.shape

(3801, 3)

geometry = [Point(xy) for xy in zip(df_point.long, df_point.lat)]
crs = {'init':'epsg:2805'}
geo_df_point = GeoDataFrame(df_point,geometry = geometry,crs = crs)

_,ax = plt.subplots(1, figsize=(15,15))
ax = creat_base_map(geo_df_point,ax)
gplt.kdeplot(geo_df_point,n_levels=25,ax=ax,shade = True,cmap='Reds',alpha = 0.6)
plt.setp(ax.get_xticklabels(), visible=False)
plt.setp(ax.get_yticklabels(), visible=False)
ax.tick_params(axis='both', which='both', length=0)
plt.show()

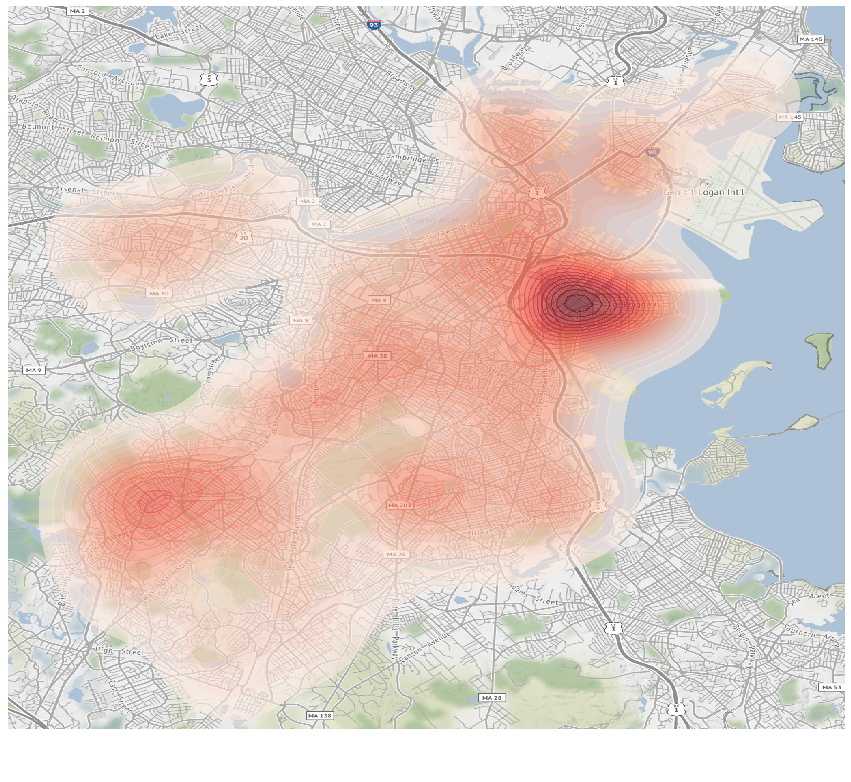
As expected, there are big pockets of build-ups in Seaport, North Dorchester, South JP, West Roxbury, and surprisingly, a big of build up in Back Bay / South End. This gives us a sense of where the developments are happening since the sheer number of constructions can drive up property price too.

New construction density weighted by declared valuation

def weighted_points(geo_df, w_col = 'w_col',print_n = False):
    weighted_points = pd.DataFrame({'lat':[],'long':[]})
    for index,i in geo_df.iterrows():
        n = int(i[w_col])
        new_df = pd.DataFrame({'lat':[i.lat]*n,'long':[i.long]*n})
        weighted_points = pd.concat([weighted_points,new_df],axis = 0)
        if (index % 500 == 0) and print_n:
            print('{} done'.format(index))
    return weighted_points

df_point_weighted = weighted_points(df_point.reindex())

geometry = [Point(xy) for xy in zip(df_point_weighted.long, permit_clean.lat)]
crs = {'init':'epsg:2805'}
geo_df_point_weighted = GeoDataFrame(df_point_weighted,geometry = geometry,crs = crs)

import geoplot as gplt


_,ax = plt.subplots(1, figsize=(15,15))

ax = creat_base_map(geo_df_point,ax)
gplt.kdeplot(geo_df_point_weighted,n_levels=25,ax=ax,shade = True,cmap='Blues',alpha = 0.6)
plt.setp(ax.get_xticklabels(), visible=False)
plt.setp(ax.get_yticklabels(), visible=False)
ax.tick_params(axis='both', which='both', length=0)
plt.show()

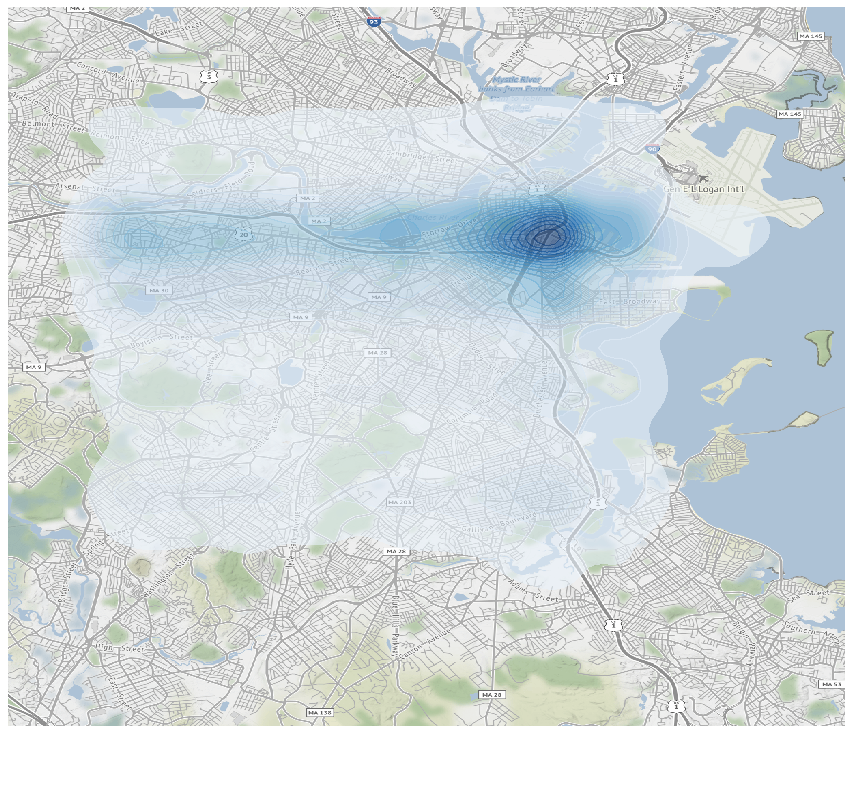
Here we see when weighted by declared valuation, downtown / Seaport area certainly overshadows the rest of the city. There high value band spans west to Fenway and south to Southie / North Dorchester.

These maps are subjected to boundary effects, hence are more likely to show high density / value in the central areas. Nevertheless, the provide another angle to investigate where developments are happening and money are flowing.